Artificial Intelligence 略して「AI」という用語が一般に出るようになって、久しくなりました。この「AI」の裏側では「ベクトル空間」の世界の中で決められた規則に則って、大量の足し算と掛け算が実行されています。
私が「ベクトル」という言葉を初めて聞いたのは高校の数学(2022年度の学習指導要領では数学C)でした。当時「ベクトル」の定義は違和感を感じる表現で、そこから「ベクトル空間」へ飛び出すのはハードルが高かったと感じていました。
今回は高校の「ベクトル」の定義に対して感じた違和感を見直すことで、「ベクトル空間」への足掛かりになるような話を書いてみます。
ベクトルとは
高校の数学で出てくる「ベクトル」は、「大きさと向きを持つ量」という定義で出てきます(厳密な表現の違いはあるかもしれません)。
図では右のように矢印(有向線分)で表現します。
「大きさ」は点Aと点Bを結ぶ線の長さを測ればいいので、【量】と考えやすいです。
一方で「向き」はしっくりきません。右から左に向いているのは分かりますが、どうにも数値では表現しづらいです。 数値で表現できない概念を【量】と定義することに、高校生の時は違和感を持っていました。
「大きさ」は点Aと点Bを結ぶ線の長さを測ればいいので、【量】と考えやすいです。
一方で「向き」はしっくりきません。右から左に向いているのは分かりますが、どうにも数値では表現しづらいです。 数値で表現できない概念を【量】と定義することに、高校生の時は違和感を持っていました。
「向き」を数値化する
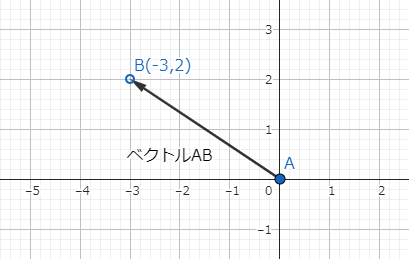
「向き」を【量】とする違和感を「そういうもの」とやり過ごしていたら、大学の時に「ベクトル空間」を扱う線形代数学で苦労することになりました。この違和感を放っていたら、「ベクトル空間」へ飛び出す時の足枷になりそうです。そこで「向き」を数値で表す方法を考えてみます。そのために、先ほどの矢印をXY座標平面に書き写してみます。話を簡単にするため、点Aは原点、点Bは整数値の座標で表現できたことにします(図1)。
右の図では、点Aから点Bへ移動するにはX軸方向に-3、Y軸方向に2移動すればよいです。
ここで、ベクトルのうち線分のみに注目して、原点から点Bまでの距離、X軸から線分ABまでの回転角が測れます。実際にやってみましょう。
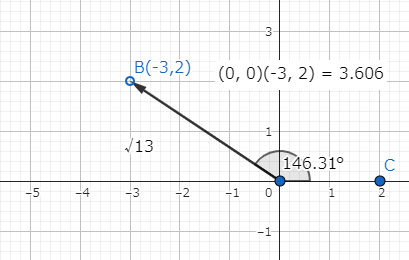
原点から点Bまでの距離:点A(原点)と点Bを結ぶ線分の長さとすれば、三平方の定理により√13≒3.606 と分かります。
X軸から線分ABまでの回転角:点Aを起点として、反時計周りに線分ABまで回転した角度を測ると、約146.31度という値がでます。
X軸から線分ABまでの回転角:点Aを起点として、反時計周りに線分ABまで回転した角度を測ると、約146.31度という値がでます。
言いたかったこと
XY座標平面を導入することで、「原点から点Bまでの距離」と「X軸から線分ABまでの回転角」が測れるようになりました。2つの測定値をベクトルの「大きさ」と「向き」とすれば、ベクトルが持つ2つの量を数値で表現できます。言い換えると、次の2つは同じ意味です。- XY座標の原点から点B(-3, 2)へ移動すること。
- XY座標の原点を起点として、反時計周りに146.31°回転した方向へ、√13分の距離を移動すること。
注意:原点を中心として回転するのは何週でもできますが、最終的に146.31°の位置で止まれば同じ方向です。ただし話を簡単にするため、回転角は0°~360°の間に限定して考えることを前提にします。
ちなみに、単にベクトルというだけでは位置は関係しませんが、片方の点を固定することでもう一方の点が決まります。そうすると、ベクトルが固定した点からの位置を表現できるようになり、「位置ベクトル」という考え方が出てきます。詳しい定義は、教科書や解説サイトに譲ります。